Why does MySQL use B-Trees instead of Binary Trees?
5 min read
While reading Database Internals, I came across an answer to a question I'd always wondered: Why does MySQL (specifically InnoDB) use B+ Trees instead of Binary Trees?
In this post, we'll explore:
- How InnoDB uses B+ Trees
- Why binary trees don't work well for databases
- How B+ Trees solve those problems
Let's dive in.
What is a B+ Tree (quick refresher)?
A B+ Tree is a self-balancing n-ary tree structure, meaning each node can have many children, not just two, like in a binary tree.
Key properties:
- Internal nodes store only keys.
- Leaf nodes store the actual data (or pointers to data).
- Leaf nodes are linked for fast range scans.
- High fanout (hundreds of children per node) keeps the tree shallow.
You could refer to the image given below to get an idea of how it looks:
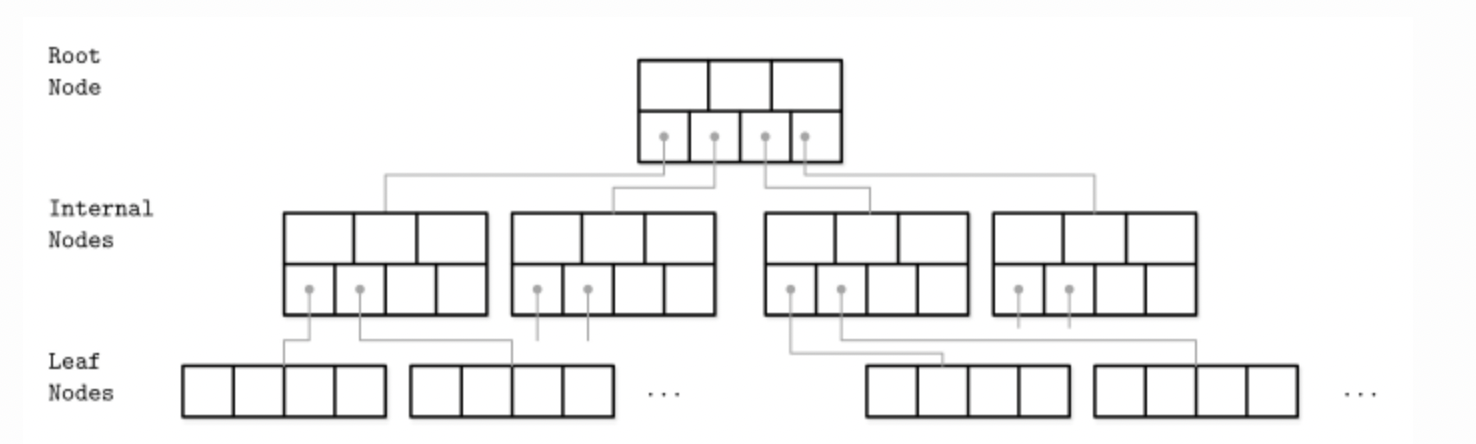
How does InnoDB use B+ Trees?
In InnoDB, every table is stored as a clustered B+ tree, ordered by its primary key. This means:
- The B+ tree is sorted by the primary key column(s)
- Each leaf node contains the full row data
- There's no separate heap. The table is the index
To fetch a row using the primary key, InnoDB walks the tree until it reaches the appropriate leaf node and retrieves the row from there.
Secondary indexes are also B+ Trees but store the indexed column(s) plus a pointer to the primary key. (I've written more on secondary indexes here)
Why binary trees don't work well for InnoDB?
Binary trees are great in-memory structures, but they fall short for on-disk storage for the following reasons:
1. Poor data locality
Each node is small and typically placed separately on disk. This means following a parent-to-child pointer may jump across multiple disk pages, causing random I/O.
2. Low Fanout = Tall Trees
With only two children per node, binary trees grow tall quickly. To locate a row, the database might have to read log₂(n) pages. This is not ideal when each read means a disk seek.
3. Rebalancing is Costly
Binary trees are more likely to become unbalanced, especially with insert-heavy workloads. To maintain balance, the tree structure must be adjusted often, which, on disk, means reading and rewriting multiple nodes across different pages. This leads to a lot of random I/O.
How do B+ Trees solve this problem?
B+ Trees were designed specifically to address the limitations of binary trees in disk-based systems. They offer several advantages that make them ideal for database indexes:
1. Better Data Locality
B+ Trees store multiple keys per node, and each node fits neatly into a disk page. This improves cache performance and reduces random I/O, as traversals touch fewer pages and stay within contiguous blocks more often.
2. High Fanout = Shallow Trees
Each node in a B+ Tree can store hundreds of keys (depending on the row and page size). This means the tree remains very shallow, even with millions of rows, usually just 3 to 4 levels deep. Fewer levels = fewer disk reads during lookups.
3. Less Frequent Rebalancing
Thanks to their high fanout, B+ Trees stay balanced naturally and require far fewer restructuring operations than binary trees. This reduces the I/O overhead.
4. Efficient Range Queries
Since all data is stored in the leaf nodes, and these leaves are linked like a linked list, range scans (e.g., WHERE age BETWEEN 20 AND 30) can be performed sequentially, without going back up the tree.
Ending notes
In this article, we explored why databases like MySQL's InnoDB use B+ Trees instead of binary trees.
I encourage the readers to explore more on the same. Here are some references:
https://dev.mysql.com/doc/refman/8.4/en/innodb-physical-structure.html
https://blog.jcole.us/2013/01/10/btree-index-structures-in-innodb/https://planetscale.com/blog/btrees-and-database-indexes
I regularly read a wide range of technical books and share my learnings here, whether it's database internals, system design, or just clever engineering ideas. Feel free to explore the rest of the blogs if that sounds interesting to you.
Thank you for reading.
Happy coding!